サンプルに「地球の陸地と海の面積比率」の計算、「一票の格差・有権者数比」の計算、 「タレントの股下・身長比率」の計算などができるデータも追加しました。 ※さまざまな比率計算に対応できるようにしたいと思っています。 「こんな比率計算のサンプルも追加してほしい」という要望このように定義される比の等式 a b = x y あるいは分数の等式 a / b = x / y を比例式という。また、連比が等しいとは、 また、連比が等しいとは、 A 1 A 2 ⋯ A n = X 1 X 2 ⋯ X n A 1 X 1 = A 2 X 2 = ⋯ = A n X n {\displaystyle A_{1}A_{2}\cdots A_{n}=X_{1}X_{2}\cdots X_{n}\iff {A_{1} \over X_{1}}={A_{2} \over X_{2}}=\cdots ={A_{n} \over X_{n}}} 基本的な比の文章題の問題です。 解き方 1 分からない方の比を でおいて考える 例)りんごとなしの値段の比が 4 :5でりんごの値段が100円のときのなしの値段 等しい比の式をかくと

三角比の問題です 青の四角部分がよく分からないので教えて頂きたいです Clearnote
比の式 計算
比の式 計算-このような、a:b=c:dという比の式を比例式といいます。 3.比を図形を使ってわかりやすく説明 外項の積、内項の積数といわれてもよくわからないと思いますので、比をわかりやすく理解するために図形を使って説明します。 下に2つの四角形があります。この2つの四角形の辺の長さの比は等しい関係にあったとすると、Xの値はいくらになるでしょうか? 比例式の例 ① 内項の積と外項の積が等しいので これを変形すると ② ①,②より A B = X Y ⋯ ① 内項の積と外項の積が等しいので A Y = B X これを変形すると A B = X Y ⋯ ② ①,②より A B = X Y ⇔ A B = X Y 中学では①式のことを 比例式 と学習します。 しかし、②式のように、 比の値 を等号で結んだ式も 比例式に含まれます 。 ここでは、主に 比の値 を用い




7 比と線分図 比例配分の問題 青空塾の教え方
比(ひ、英 ratio )とは、2つ(または3つ以上)の数の関係を表したもの。 数 a, b について、その比は ab で表され、「a対b」とよむ。a を前項、b を後項(こうこう)という。また、前項と後項を入れ替えた ba を元の比の逆比または反比という。3数以上の場合も abc のように表し、特に連比比の値を使って、比の計算規則を導(みちび)いてみましょう。 a:b=2:3 の式を比の値で表すと、 左辺は a/b、右辺は 2/3 なので、 a/b=2/3 両辺に 3b をかけると、 3a=2b となります。 つまり、a:b=2:3 は、3a=2b と同じです。 規則 a:b=n:m ⇔ am=bn (外側の積=内側の積) 例題 比の「:」記号を「÷」に置き換えたら比の値になります。 A:B A : B の比の値はA ÷B=A B A ÷ B = A B 基本2同じ数字で掛けたり割ったりしても比の値は変わらない 2:3 2 : 3 という比を表すそれぞれの数字に、同じ数をかけたり割ったりしても比の値は変わりません。 比の値は2つの数字をそれぞれ分母と分子にした分数と考えられますが、分母と分子に同じ数をかけても
三角比の方程式や不等式、二次関数の定番問題を扱いました。 重要なものばかりなので、全ての問題を解けるようにしておきましょう。 今回扱わなかった面積関連の問題は、次の記事で扱っています。 こちらもあわせてご覧ください: 前の記事;比例式(ひれいしき)とは、比あるいは連比に関する等式のことである。 A に対する B の割合が、X に対する Y の割合に等しいとき、 AB=XY と書く 引用: 比例式について wikipedia 用途: 画像の比率計算や個人的なゲームのレベルアップまでの時間計算など色々使ってる。 例の式 4000=x100 0x=4000 x=4000/0 例えば、ABスーパーに"肉屋""魚屋""米屋"があったとします。 ABスーパーの今月の売上高は、2,000,000円でした。 肉屋は850,000円、魚屋は550,000円、米屋は600,000円でした。 その時の各構成比を計算してみます。 肉屋 = 850,000円 ÷ 2,000,000円 = 0425 (425%
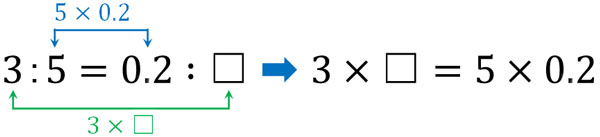
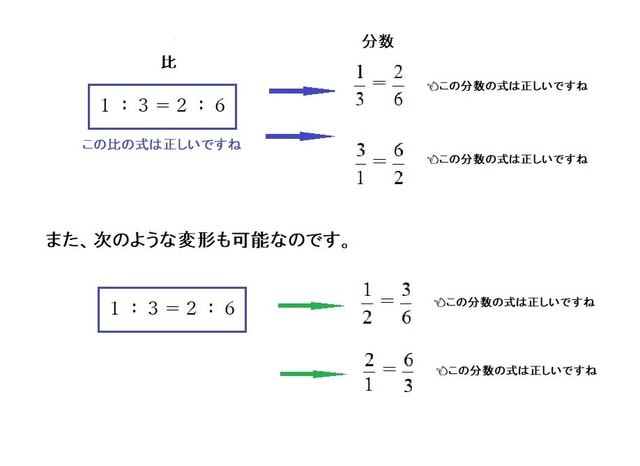
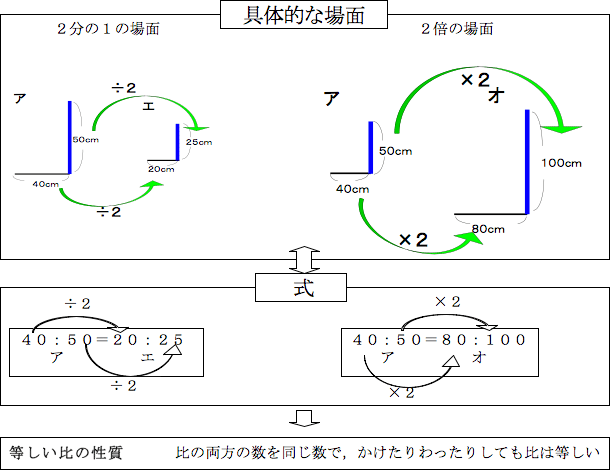
比例式 比は、小学生のときにも見ましたが、\ 12 \などと表されるものですね。例えば、「 x と y の値は $12$ だ」といえば、「 y を基準にしたときの x の割合は、 $2$ を基準にしたときの $1$ の割合(=05)と等しい」という意味で、簡単に言えば、「 y は x の2倍 」という意味になり比率の計算 計算式の入力 「農業産出額」の「構成比」を表示させましょう。表示形式はパーセント表示、小数点以下を第1位まで表示させましょう。 「構成比」とは、合計に対してそれぞれの品目の金額が占める割合のことです。 金額÷全体の合計=構成比 比"3 9″は両方の数を3で割れば、"1 3 ″になりますね。 よって、比"1 3″と比"3 9″は等しいことになります。 つまり、 1 3 = 3 9 といえます。 このとき、比例式の外側の数である1と9をかけると、9になります。 また、比例式の内側の数である3と3をかけると、9になります。 このよ




比例式 比の値 教遊者



比の計算と比例式 整数 小数 分数の比と文章問題 Hatsudy 数学 科学
こんにちは、ウチダです。 今日は、中学1年生で習う 「比例式」 について、まず分数を用いた計算方法からある重要な公式を導き出します。 また、記事の後半では、かっこを含む比例式の計算を要する文章問題なども解説していきます。 比例式とは 比例式三角比の相互関係の 3 3 つめの式 tan2 θ 1 = 1 cos2θ tan 2 θ 1 = 1 cos 2 θ も利用できそうです。 これを式変形していくことで、解決することもできますが、 そもそも、 tan2 θ 1 = 黄金比の定義と見ることもできます。数学の諸分野や自然界に黄金比が登場するのは,全て性質1が元になっています。 すなわち,なんらかのシステムが x 2 − x − 1 = 0 x^2x1=0 x 2 − x − 1 = 0 という方程式の 成立を要求するときに,そのシステムに黄金比が登場します。様々な場面で黄




三角比の問題です 青の四角部分がよく分からないので教えて頂きたいです Clearnote




7 比と線分図 比例配分の問題 青空塾の教え方
比エンタルピーを求める計算式で、 とある例題では、 理想空気、体積一定、密閉容器で 加温した場合のエンタルピー変化をもとめよ では Δh=m*Cv*ΔT 別の問題では 理想空気、容積一定、密閉容器で 加温した場合の比エンタルピーをもとめよ では Δh=Cp*ΔT で計算されています。三角比の式の値は入試や模試などでよく見かける問題です。 和、差が与えられているときには両辺を2乗して積を求めることができる。 この考え方と式の変形について覚えておけば楽勝な問題です。 サクッと解けるように練習しておいてくださいね(/・ω・)/比の計算の解説 比は、その比に同じ数を掛けるか割った別の比と同じという性質を持っています。 12 = 24(左の比に2を掛けたのが右の比) 36 = 12(左の比を3で割ったのが右の比) 比の関係は分数の関係によくにています。 分数の場合も、分母と分子に同じ数を掛けるもしくは割った分数と同じです。 約分したら同じ分数になるということですね。 1 2 =



超重要 中学数学の分数準備7 比と分数 算数の教え方教えますmother S Math Happy Study Support




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo
前年比や伸び率(増減比)の意味と求め方定義 それではまず、前年比の定義について確認していきます。 前年比とは売り上げ、利益、販売個数などの項目において、ある対象の年の数値に対する一つ前の年の数値との比といえます。 計算式としては比は、 同じ数をかけたり、同じ数で割ってたりしても同じ比 になります。 例えば、「32」の両方を2倍して、「64」と書いても同じものです。 逆に、「164」は、どちらも4で割って「41」と書いても同じ比になります。 この性質を利用して、 比はなるべく小さな整数で書く というのが決まりになっています。 例えば「2412」を、そのまま答えに書いてしまうと となり,比の式を立てることなくACの長さを直接求めることができるようになる。 ここで $\dfrac{3}{5}$ は $\text{AC}\text{AB}$ の比の値を表すが,これは $\sin\theta$ であるから, \begin{align*} \text{AC}=\text{AB}\sin\theta \end{align*} となる。「比」や「割合」をしっかりと理解・活用している人は,三角比を




比の計算問題 比を簡単にする方法は小学生でもできる 中学や高校の数学の計算問題




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
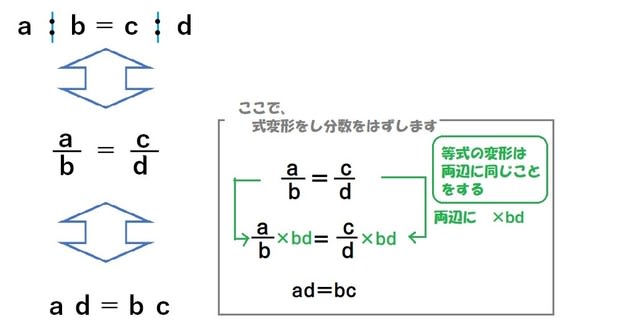
比率の方程式とは、数(文字)の比を等式で示したものです。比率の方程式は「ab=cd ⇒ ad=bc」のように変形できます。3つの比率の方程式の解き方など、下記も勉強しましょう。 比例式とは?1分でわかる意味、問題と解き方、3つの場合、分数との関係 3つの数の比率と計算は?3分でわかる比例式とは下のような2つの比が等しいですよ、 ab = cd ということを表した等式のことですね。 どういうときに2つの比が等しいっていえるかというと、比の値が等しいときなんです。 比が ab のとき 比の値は a/b になります。 すると、左辺の「ab」の比の値は「a/b」、右辺の「c d」比の値は「c/d」になります。 つまり、「a b = cd」となるときは2つの比の値が 異なる三角比の間には、次のような関係が成り立ちます。 一つ目の式は正接( tan )の定義から直ちにしたがうものです。 二つ目の式は、三平方の定理を用いると証明できます。 先ほどの図で が成り立つことを用いましょう。 三つ目の式は、二つ目の式を で割り算したものです。 90º θ や 180º θ の三角比 90º θ や 180º θ の三角比の計算をおさらいします。 単位円を描いて、上




数学 三角比の式と値の求め方とコツ 教科書より詳しい高校数学




比率の計算
上記の式から、 各カテゴリーの売上構成比をすべて足すと、1になる ことがわかります。 売上構成比の計算(例) 食品の売上100万に対して、各部門の売上は以下の通り。比例式の解き方 比例式の性質 x y = 3 5 のように比が等しいことを表す式が 比例式 である。 比の性質から「等しい比の比の値は等しい」ので、 a b = m n なら a b = m n である。 両辺に bnをかけると an = bm となる。 ある材質の導電率(電気伝導率)は2 × 10^7 S/mです。この材料の比抵抗(抵抗率)はいくらと求められるでしょうか。 解答2 こちらでも上の導電率と比抵抗の換算式を元に計算していきます。 両方とも良く使用する用語であるため、しっかりと覚えておくといいです。 まとめ 電気伝導率
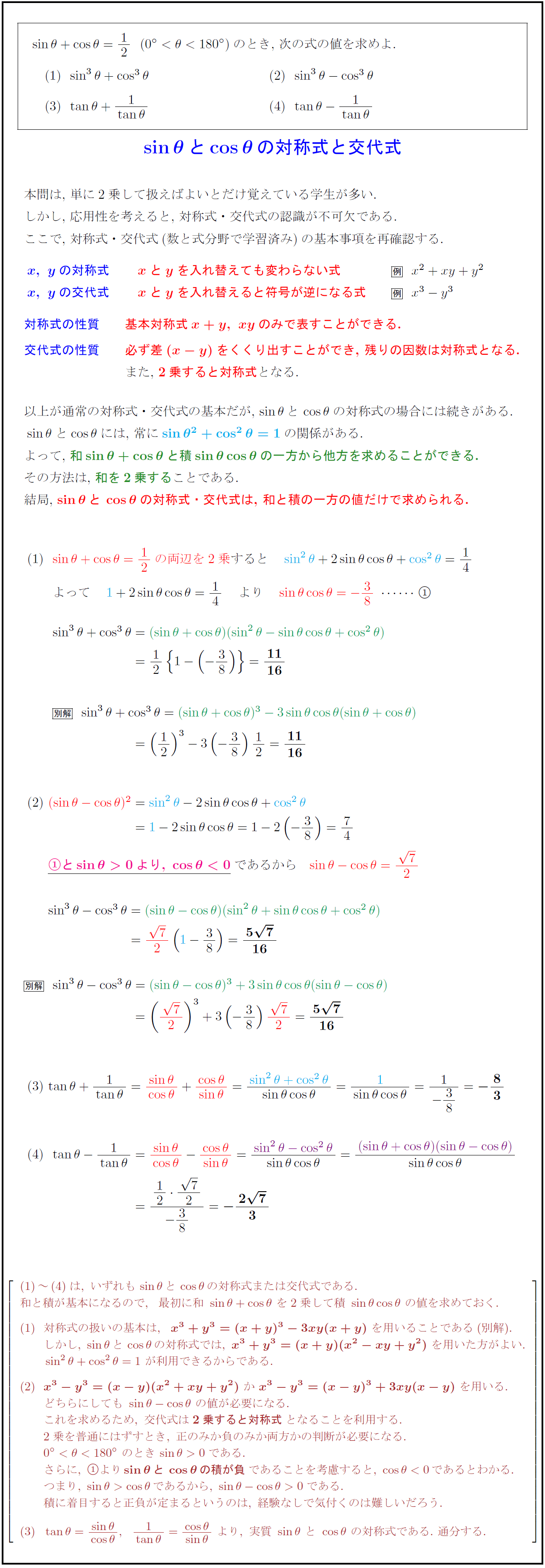



高校数学 Sin8とcos8 Tan8と1 Tan8の対称式 交代式の値 受験の月




計算問題に最適 コレダケ でわかる 比 の使い方 がんばれ看護学生 メディックメディア
下の表の「前年比」と「伸び率」の場所を求めてみます。 では、計算式を入れましょう。 「前年比」からいきます。 「f3」をクリック して、計算式のスタートである 「=」を自分で入力 します。 まず最初に、 「今年度実績」の場所をクリック します。比の方程式 内項の積 = 外項の積 A B = C D B × C = A × D 1 3 = x 12 の時の x を求めなさい 1 3 = x 12 3 × x = 1 × 12 3 × x = 12 3 に何をかけ算したら答えが 12 になるか考えます。 3 × 4 = 12 ですね。 すなわち x = 12 ÷ 3 です。 x = 4 比例式とは、 左辺と右辺の比(または比の値)が等しいことを示す式 です。 比例式の定義 に対する の割合が、 に対する の割合と等しいとき、 比または比の値を使って と表せる。 上記の等式を「比例式」という。 比 数量の割合を のように表したもの。 特に、 つ以上の数の比は「 連比 」という( など)。 また、, は「比の項」という。 比の値 比の後項に対する前項の割合(前項 後項
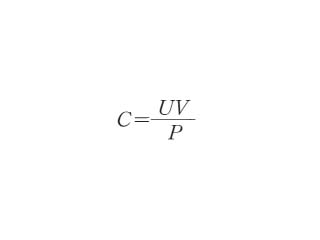



クリアランス比の公式とは コトバンク




比率の計算
今回は、比の値の求め方について書いていきたいと思います。 比の値とは? 比の値を求める問題 問題① 問題② 問題③ 比の値とは? a:bという比があったとき、前項aを後項bで割ったが比の値になります。比の値=前項÷後項後項を1としたときに、前項がどのくらいにあたるのかを表して 三角方程式の出題パターンまとめ 置き換えを利用する三角方程式(Type1) 三角関数を置換する時の注意事項 三角比の相互関係を使うタイプ (type2) 単位円を使ってθを求める 2倍角の公式を利用する(type3) コサインの2倍角を利用する(要注意) 三角関数の比例式とは12=24のように、数の比を等式で示したものです。 2つの比だけでなく、3つの比を等式で表すことも可能です。 また比例式ab=cdは、ad=bcに変形できます。 例えば12=24⇒1×4=2×2ですね。 今回は比例式の意味、問題と解き方、3つの比の計算、比例式と分数の関係について説明します。 「比」の計算、3つの数の比は下記も参考になります。 比率とは? 1




解説の上から4行目の 比の式 って 右辺の 2 って長さじゃなくて Clearnote




等差 等比 の和 2次式 等比 の和 おいしい数学
よって、比例の式は $$\color{red}{y=2x}$$ となります。 比例の式を作りたければ、\(y=ax\)の形を覚えておいて、そこに\(x, y\)の値を代入するだけでOKですね。 比例の式グラフから式を作る中学校数学で出題される比例式の問題は、比の等式の一部に文字が含まれるようなものです。 これを解くには主に比の性質の3つ目、 「内側と外側の積が等しい」 ということを利用します。 具体的に見てみましょう。 次の比例式の解を求めよ。 x:5=9:15 x : 5 = 9 : 15 外側の積( 15× x=15x 15 × x = 15 x )と内側の積( 5× 9=45 5 × 9 = 45 )が等しいので、「 15x=45 15 x = 45 」という 中1数学「比例式の文章題(利用)」です、比と比例式 比の値比abで, a, bを比の項といい, 前の項aを後ろの項bでわった値 を比の値という。 比例式ab=cdのような,比が等しいことを表す式。比例式にふくまれる文字の値を求




高校数学無料問題集 数 第3章 図形と計量 三角比の拡張と相互関係の式 桝 ます Note
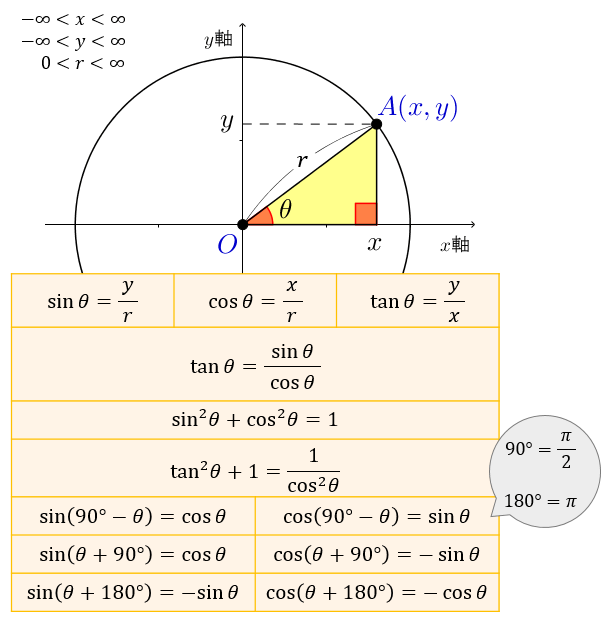



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ




数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




小6 算数 小6 15 比と比の値 Youtube




こんにちは 新高校一年生です 三角比の相互関係の公式について質問です Clearnote



3




三角比の相互関係の式を使ってサイン コサイン タンジェント やってみよう 都立入試の情報満載 こじんまりしたこじま塾ブログ




比率の計算
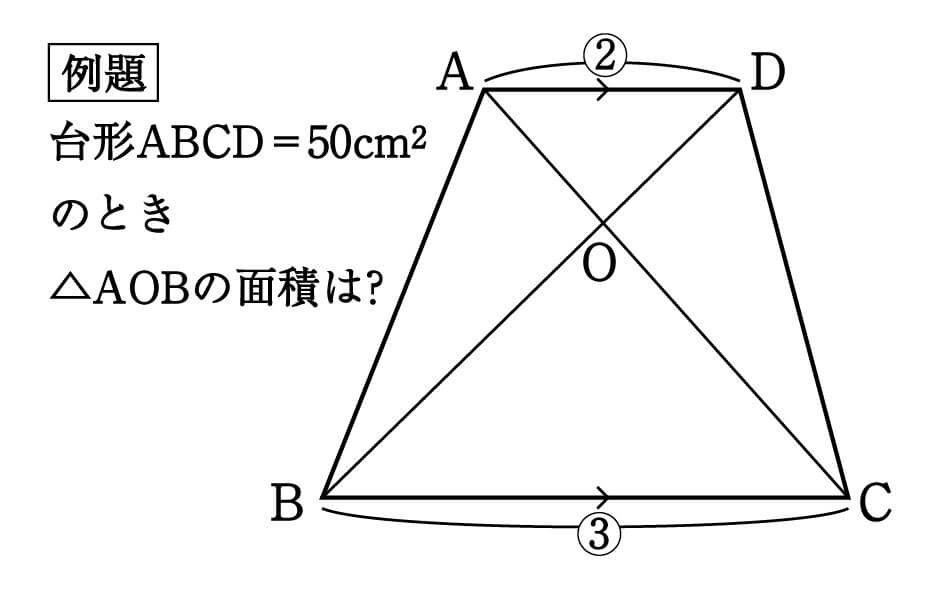



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト
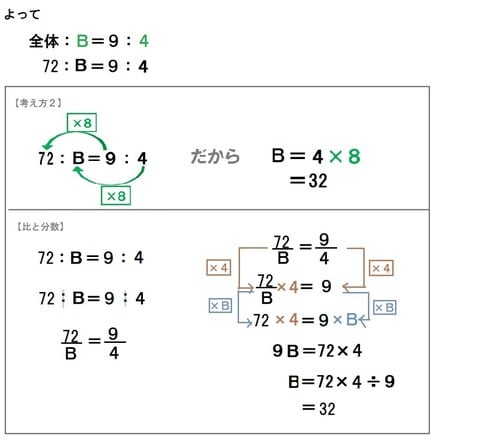



比の問題 小6 比と分数の関係 算数の教え方教えますmother S Math Happy Study Support
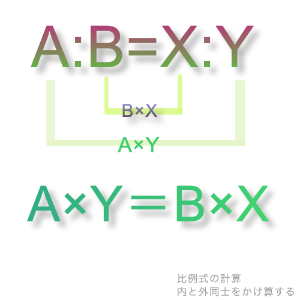



比例式 Xを求める計算ツール




比の計算問題を実践練習
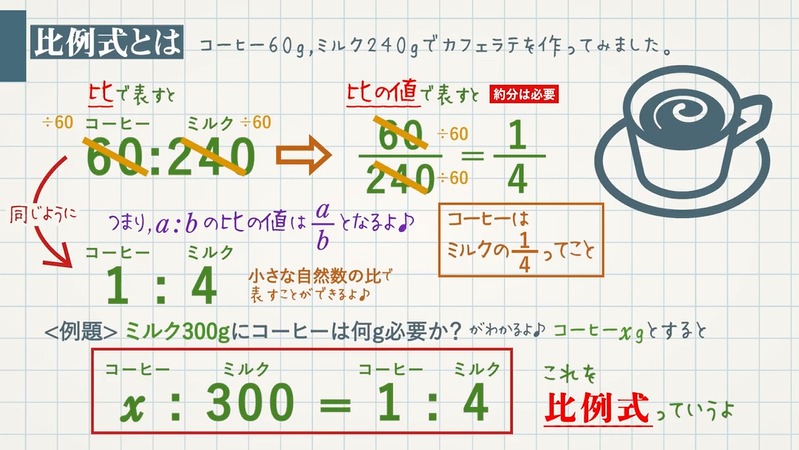



比例式 比の値 教遊者
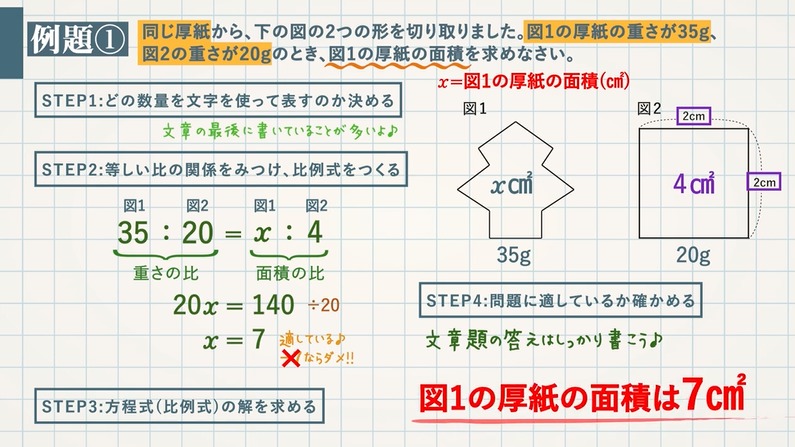



方程式の利用 比例式で解く 文章題の基本問題 教遊者
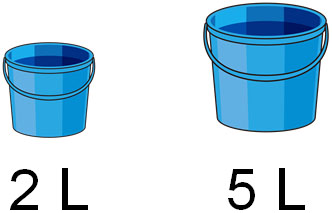



比の計算と比例式 整数 小数 分数の比と文章問題 Hatsudy 数学 科学
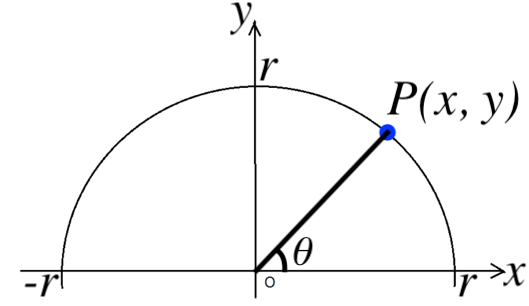



三角比を用いた計算問題をマスターしよう スタディクラブ情報局



算数実践実例集 啓林館
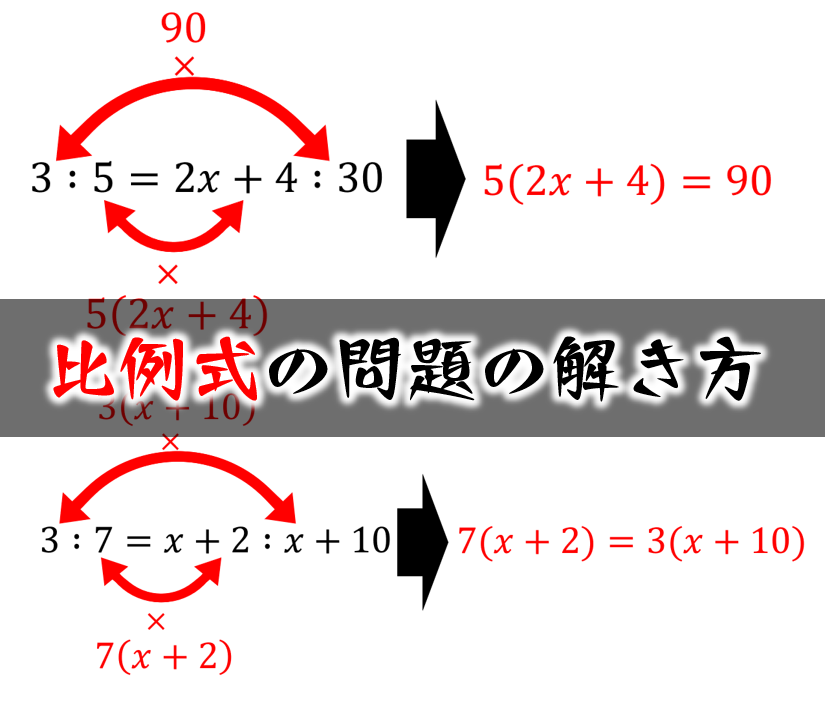



比例式の問題の解き方 数学fun




比の計算 デキる人は自然にやっている比例式の上手な計算方法 子供から大人まで動画で脳トレ 楽天ブログ



3
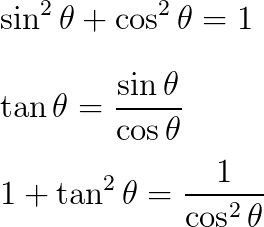



三角比の公式まとめ サイン コサイン タンジェント 正弦定理 余弦定理など Irohabook




比 の 連立方程式 の巻き 名寄 算数数学教室より




これらの問題なのですが 解説を読んでも全く理解出来ませんでした もっと噛み砕 Clearnote




高校数学無料問題集 数 第3章 図形と計量 三角比の拡張と相互関係の式 桝 ます Note
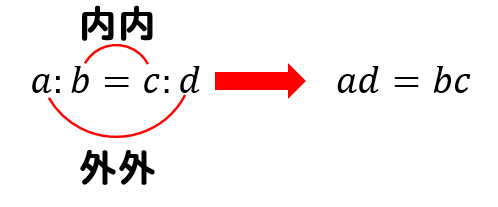



比例式の解き方は かっこがついている式の計算方法は 数スタ
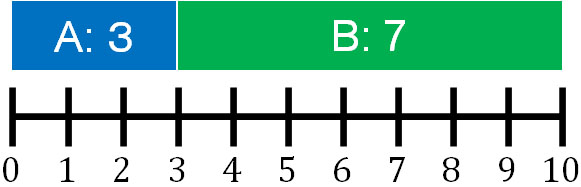



比の計算と比例式 整数 小数 分数の比と文章問題 Hatsudy 数学 科学
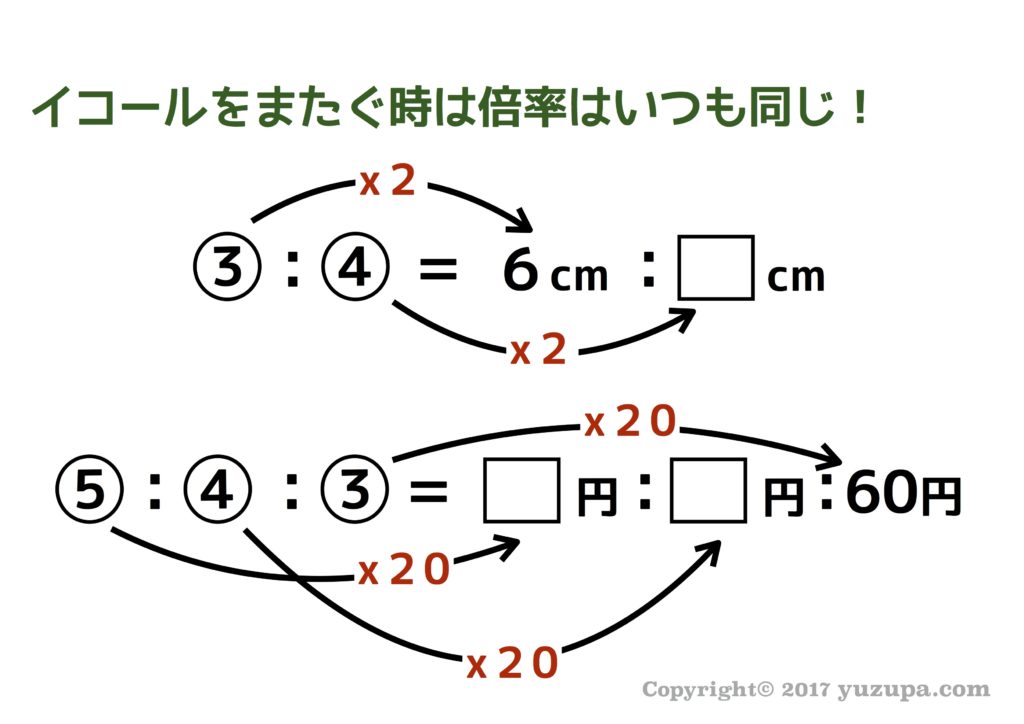



中学受験 割合と比は 7つ道具 で克服 かるび勉強部屋




小6 比 比の計算 比を用いて面積を求めよう 日本語版 Youtube
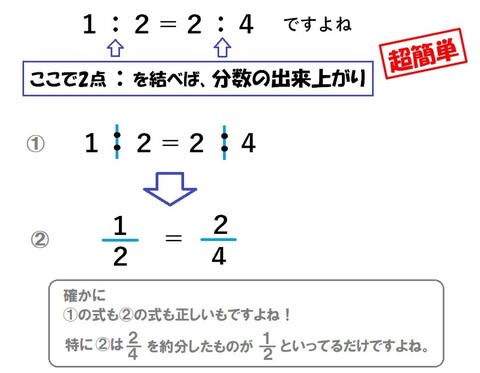



比と分数の関係 小6 超重要で超簡単 比 分数の変形 算数の教え方教えますmother S Math Happy Study Support




比と比の値についての自主学習ノート例 家庭学習レシピ



2




高校数学 余角90 ー8の公式と補角180 ー8の公式の証明と強力な覚え方 三角比の等式の証明 Sin A B 2 Cosc 2など 受験の月




例題 三角比と式の値 Youtube
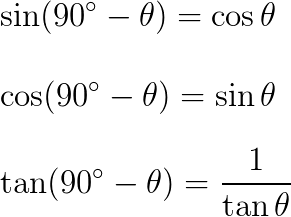



三角比の公式まとめ サイン コサイン タンジェント 正弦定理 余弦定理など Irohabook



Studydoctor比の値と比例式 方程式 中1数学 Studydoctor




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo
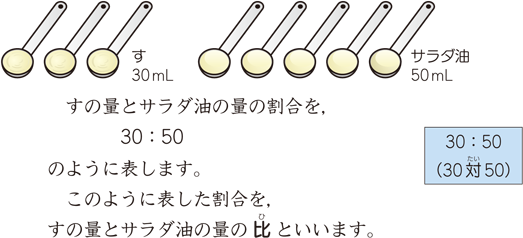



比と比の値 算数用語集
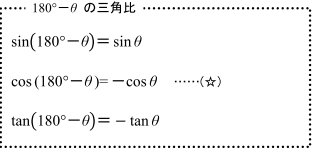



180 8の三角比 数学 苦手解決q A 進研ゼミ高校講座




高校数学 数 77 三角比 公式編 Youtube




三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ




三角比を用いた計算問題をマスターしよう スタディクラブ情報局



Studydoctor三角関数の式と値 高校数学 Studydoctor
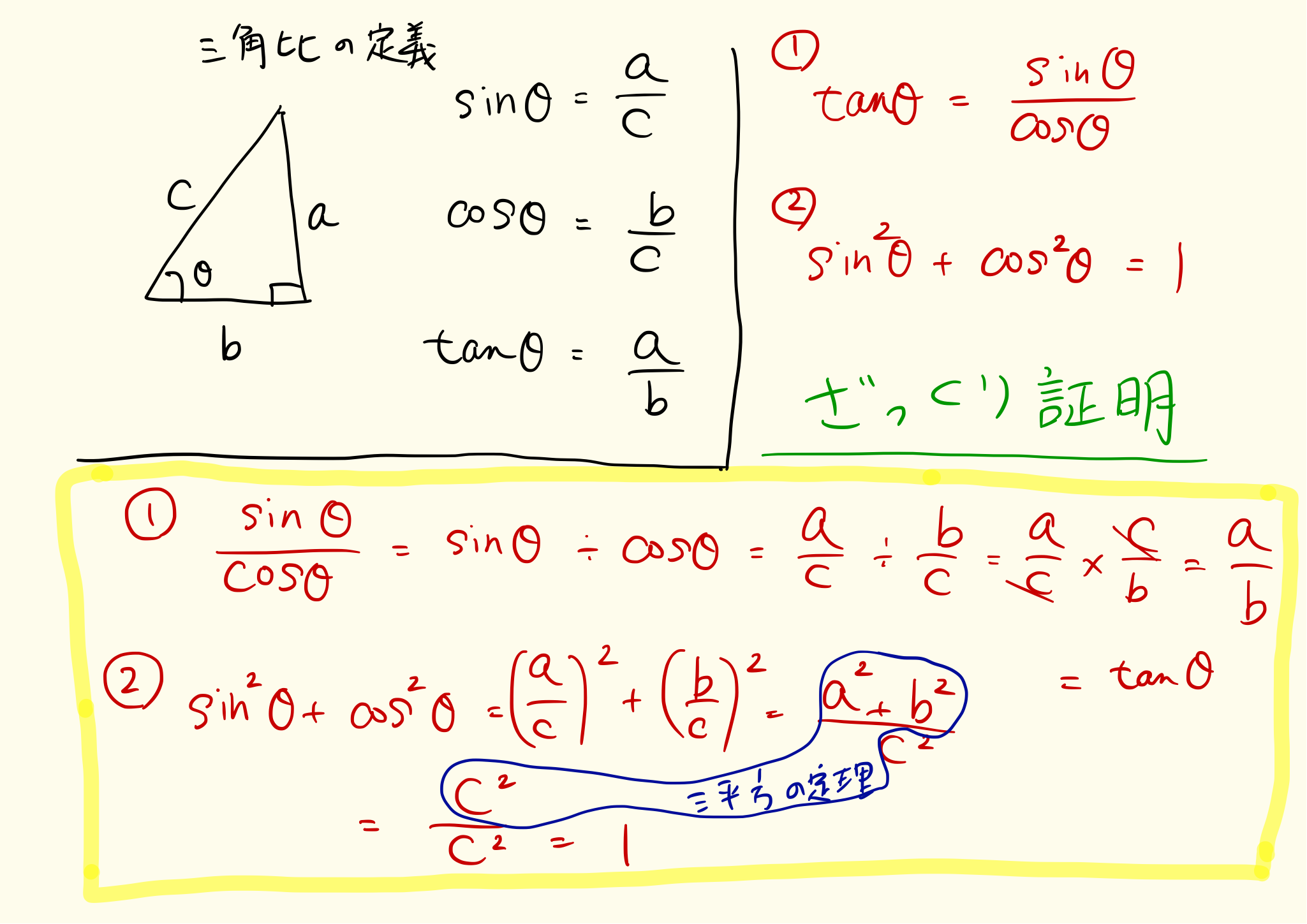



三角比の公式まとめ サイン コサイン タンジェント 正弦定理 余弦定理など Irohabook




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun




比率の計算




比の性質を解説 比例式や連比の解き方だってこんなに簡単
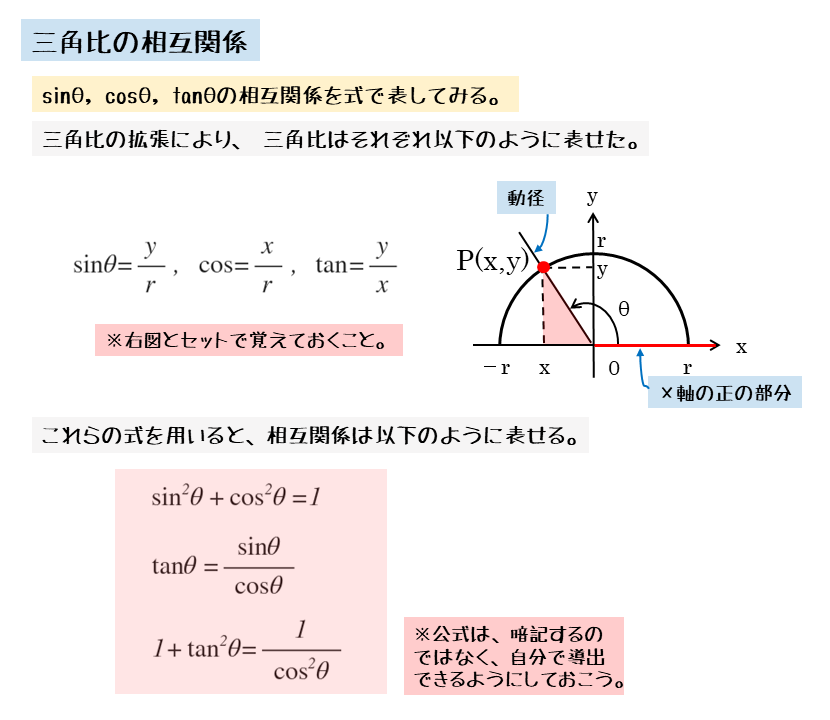



図形と計量 三角比の相互関係について その1 日々是鍛錬 ひびこれたんれん



比と分数の関係 小6 超重要で超簡単 比 分数の変形 算数の教え方教えますmother S Math Happy Study Support



3



6年生 算数 まとめ テスト 答え




数列 黄金比 を計算する方法 大人が学び直す数学
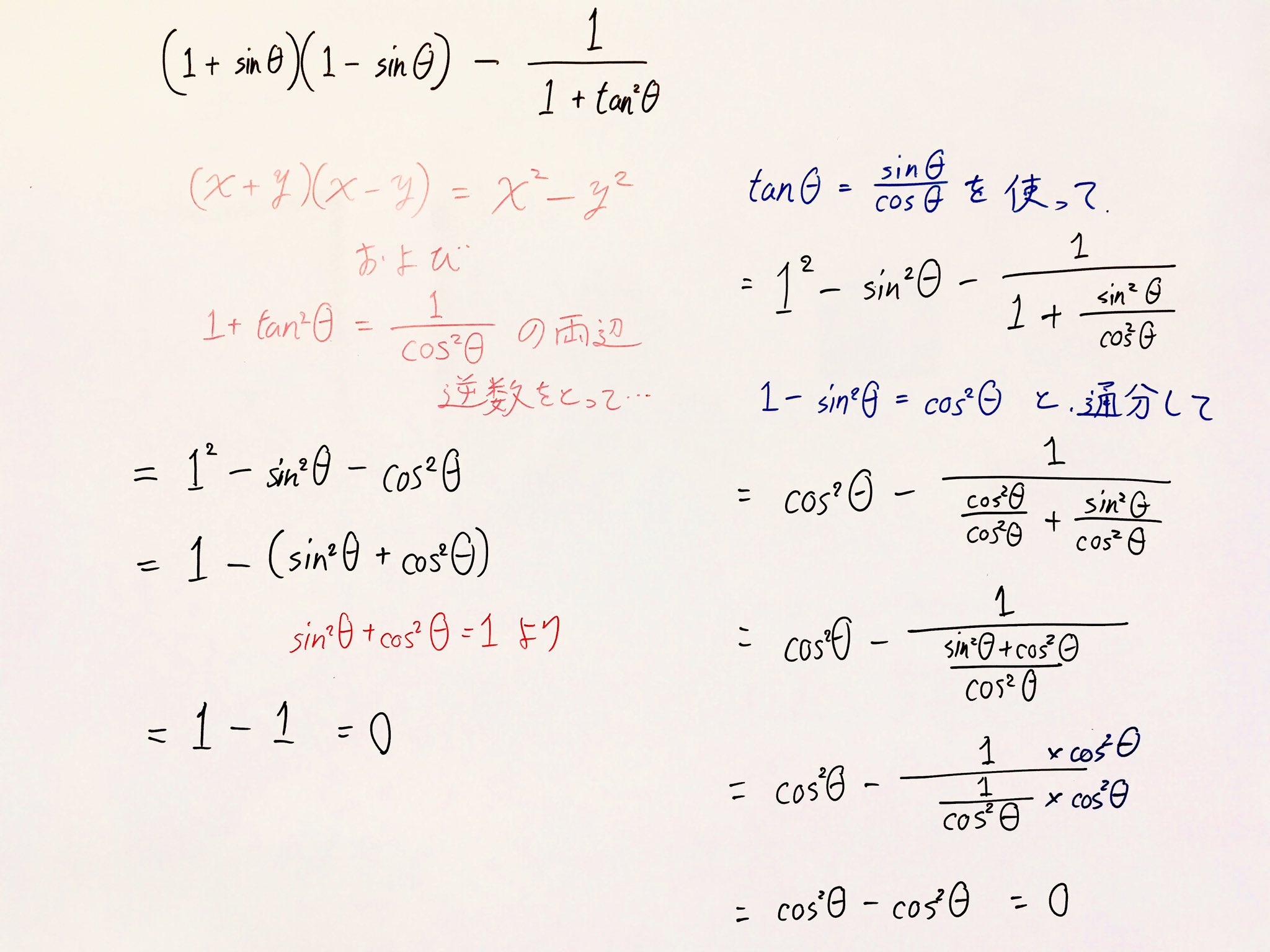



Twitter 上的 塾長 個別指導塾forward 数学ia 三角比 の計算 Tan二乗とcos二乗の公式 を使った解答と 使わない解答 使わないと変形が面倒だが できる 三角比の式は色々な崩し方があるので 模範解答にとらわれず色々な解き方を試してみよう 公式は忘れては




勉強しよう数学解答集 三角形の3頂点のベクトルの張る三角形の面積比の公式
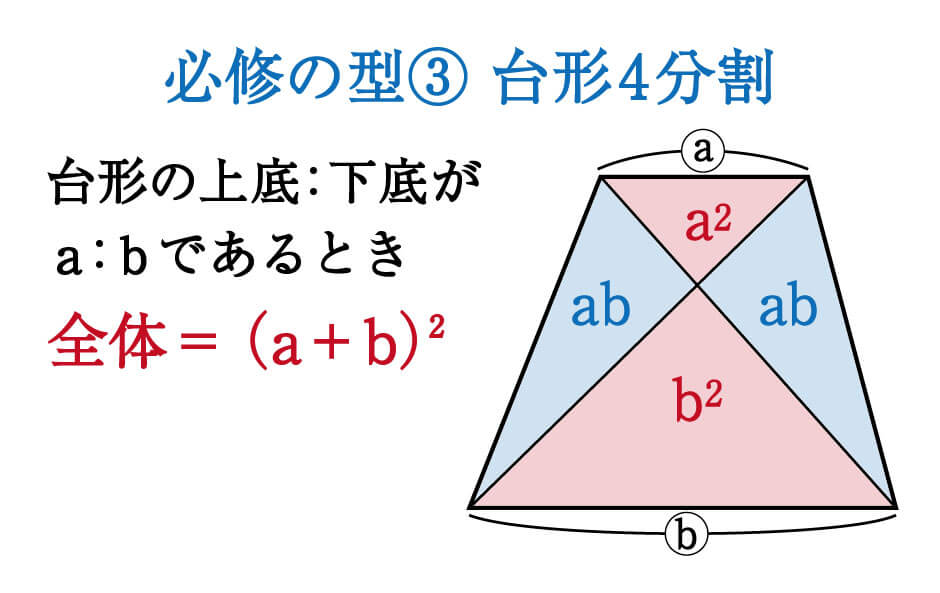



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




恋する中高一貫校 適性検査 教材クリエイター 比の問題 公立中高一貫校適性検査 18年 千葉市立稲毛高等学校附属中学校 数学教室 小学校 算数 中学 勉強
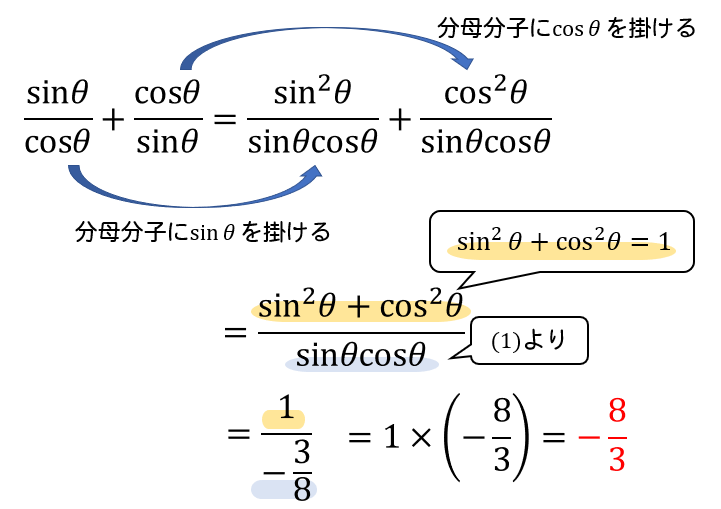



数学 三角比の式の値を求めよ 隠れた条件を見落とすな 数スタ
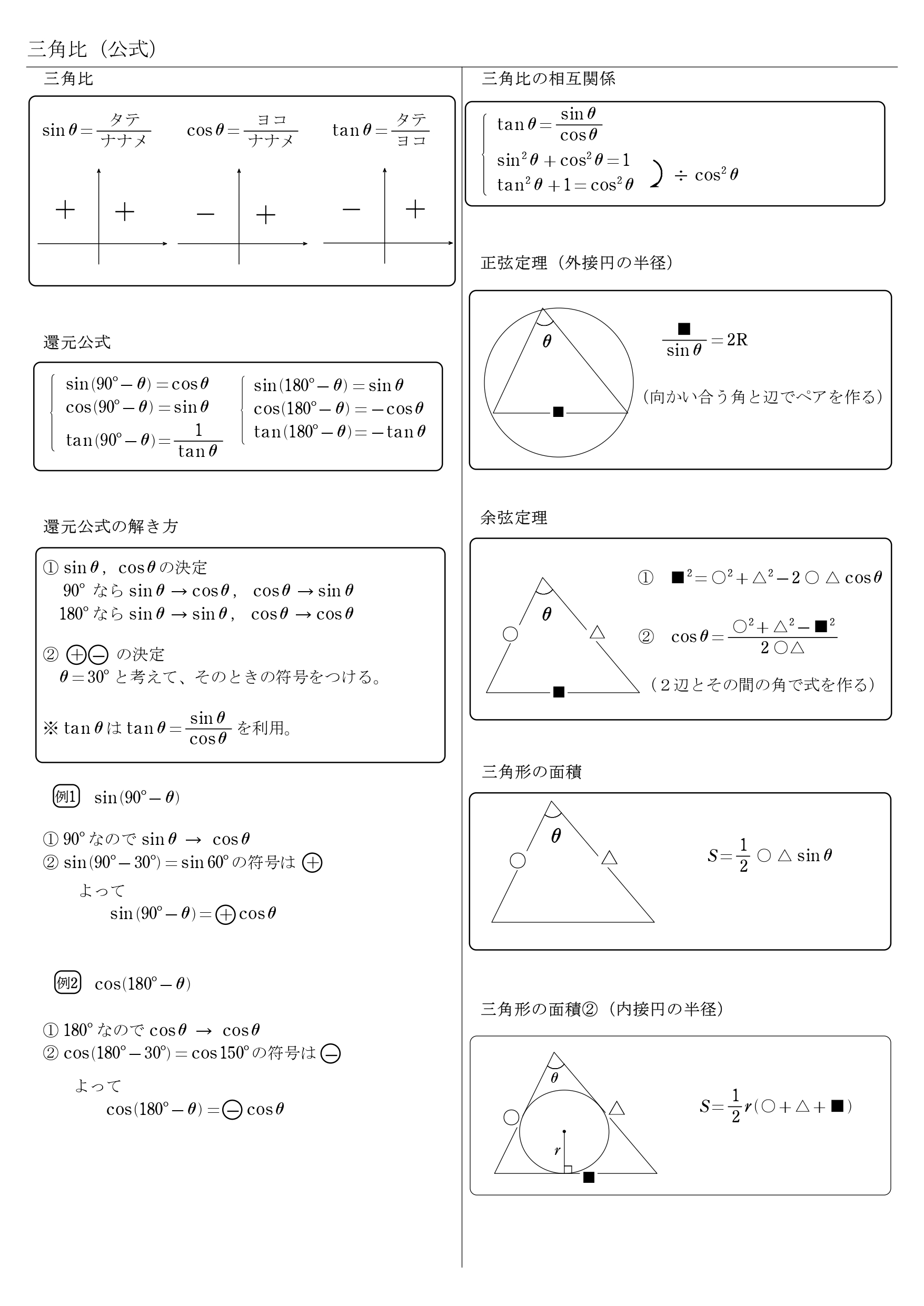



高校数学 三角比 Sin Cos Tan 公式一覧 変換 正弦定理 余弦定理 面積 学校よりわかりやすいサイト



比の計算と比例式 整数 小数 分数の比と文章問題 Hatsudy 数学 科学




Cos8とsin8の順番が最後に変わっているんですけど これってどちらから書 Clearnote




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo




比例式の性質 3分でわかる 比例式の解き方 Qikeru 学びを楽しくわかりやすく




すきるまドリル 小学6年生 算数 比と比の値 比と比の利用 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント



Studydoctor三角比の相互関係と計算 高校数学 Studydoctor



6年算数比とその利用 わかる教え方1




数列 黄金比 を計算する方法 大人が学び直す数学
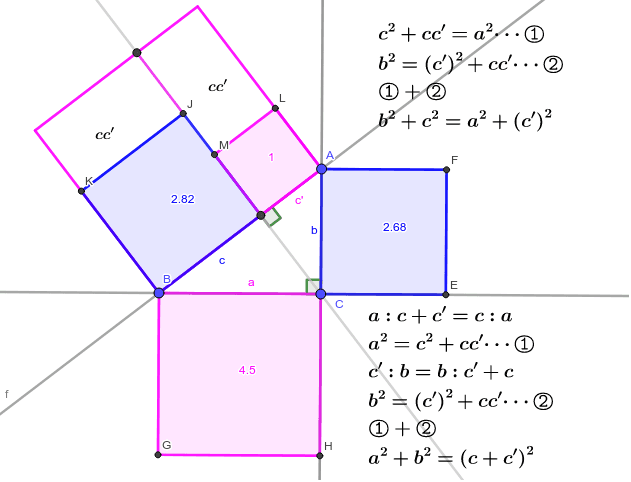



ピタゴラスの定理の拡張 その2 Geogebra




三角比の問題です 青の四角部分がよく分からないので教えて頂きたいです Clearnote
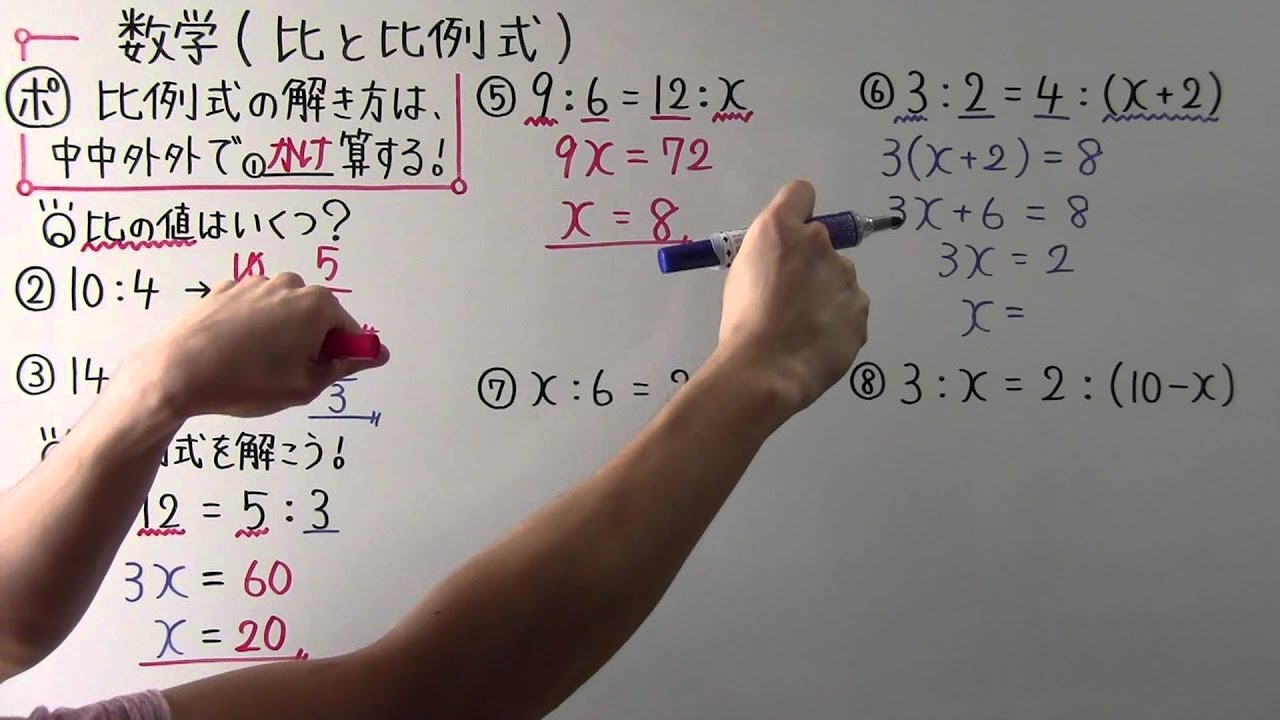



中1 数学 中1 32 比と比例式 Youtube




比例式の問題の解き方 数学fun
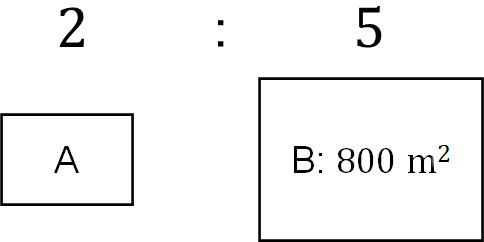



比の計算と比例式 整数 小数 分数の比と文章問題 Hatsudy 数学 科学
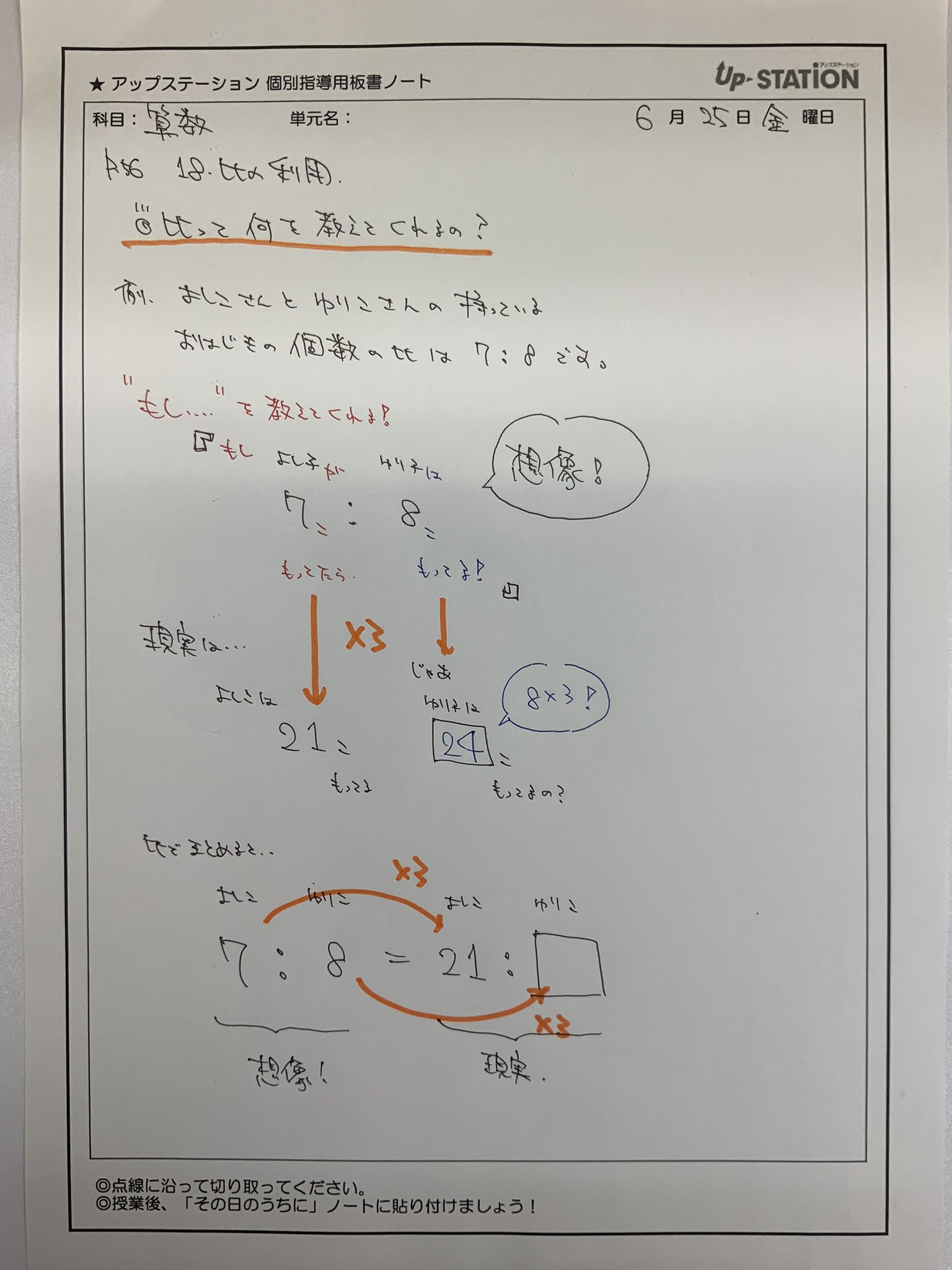



個別指導塾 アップステーション 小6算数 比の利用 比の文章題を解いているときに どんなことを考えていますか ただ闇雲に 比の式を立てて解くのではなく 問題文を読んで頭の中でイメージをもてるといいですね 個別指導 アップステーション 算数




中1数学 比と比例式 比の値 とはなんだろう Qikeru 学びを楽しくわかりやすく




割合との違いや比ならではの特徴をしっかり覚えよう 比の性質 基礎編 中学受験ナビ




数学 三角比の式の値を求めよ 隠れた条件を見落とすな 数スタ
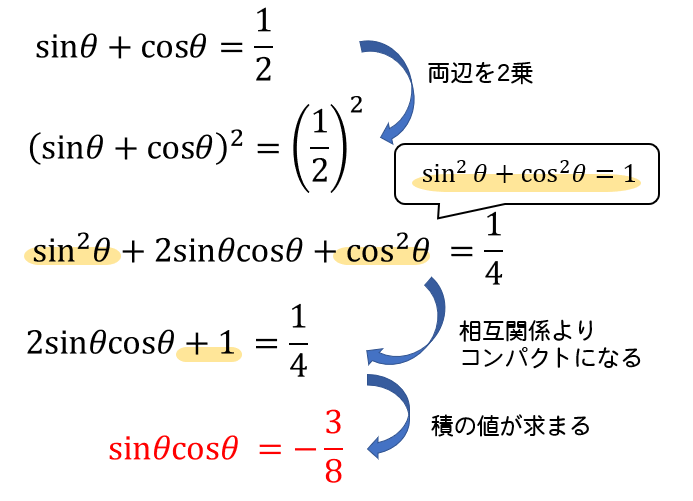



数学 三角比の式の値を求めよ 隠れた条件を見落とすな 数スタ




比例式 比の値 教遊者
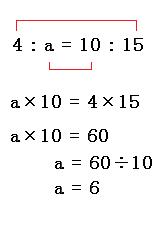



比の性質を解説 比例式や連比の解き方だってこんなに簡単




高校数学b 等差 等比 型 2次式 等比 型の数列の和 受験の月




オッズ比 疫学用語の基礎知識
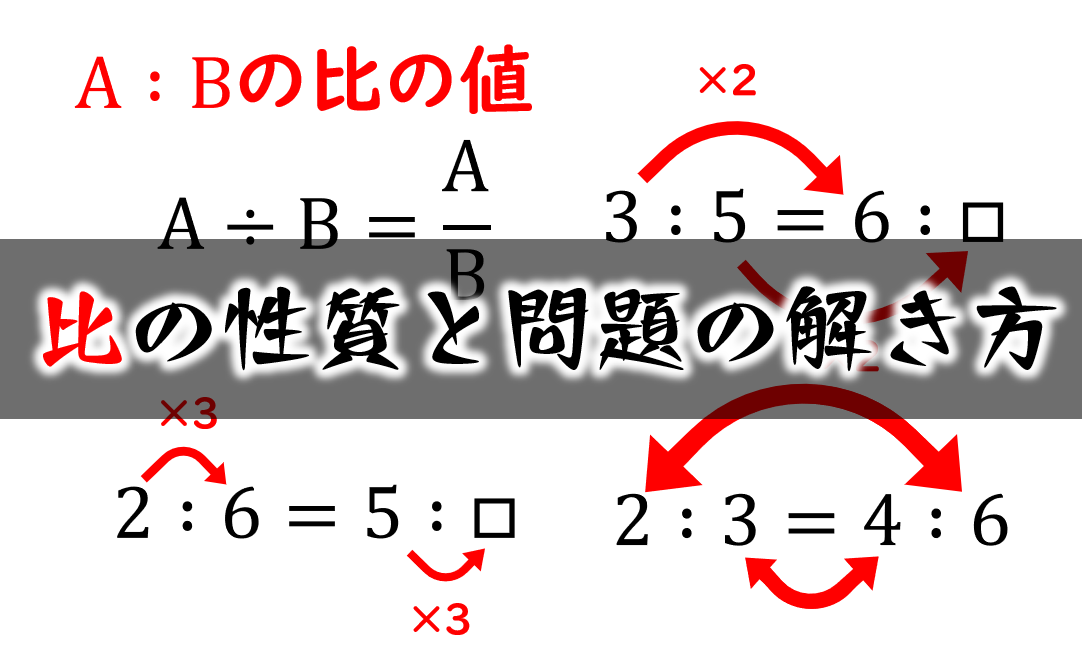



比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun




三角比の相互関係の公式4つって 証明 覚え方 応用問題6選を解説 遊ぶ数学




割合との違いや比ならではの特徴をしっかり覚えよう 比の性質 基礎編 中学受験ナビ




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun




比の値と比例式 方程式 中1数学 Youtube




30 三角比の相互関係 式の値 の解き方を教えてください Clearnote




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




比と比の値 その2 家庭学習レシピ


