正三角形の問題を速攻で解くための2大公式 高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる"秒殺テクニック"を紹介していきます。 今回のテーマは正三角形の2大公式です。 これらの公式をおぼえれば、正三角形の高さと面積を瞬間的に出すことができます円の面積を求める公式は小学校で習いますが、なぜその公式になるのか?という 疑問 (ぎもん) は、高校2年生で 微分 (びぶん) を学習するまで分かりません!下のリンクでは、図形的に公式を 理解 (りかい) してもらう方法を 紹介 (しょうかい) しています。 扇形 (おうぎがた) の面積も 重要 相似比と面積比,体積比の公式の証明 レベル ★ 基礎 平面図形 更新日時 相似な平面図形について,面積比=相似比の二乗 相似な空間図形について,体積比=相似比の三乗 面積比をきちんと理解できれば体積比もほぼ同様に理解できるので

Amc 10 第一讲 数学中的面积公式都是怎么来的 知乎
面積 比 公式
面積 比 公式- よって、面積は相似比の2乗=面積比より、1:4となる。 (2)の解説 最初の公式 を利用して、今回も解くことになります。点bと点eを結ぶことで利用できます。よって、上の図示のように agdと四角形gbceの面積比は、2:5となります。 解答 (1) agd面積比は相似比の2乗。 体積比は相似比の3乗。 相似比がabの相似な図形の場合 辺、高さなど 長さの比は a b 表面積など 面積比は a 2 b 2 体積比は a 3 b 3 例 相似比23の相似な円柱PとQがある。 2h 2r 3r 3h Pの底面の半径を2rとするとQの底面の半径は3r Pの高さを2hとするとQの高さは3h ①表面積




一道面積比公式的另證 的回響 用三角形的a S A 面積公式
abcをadで切り分けた abdと adcは高さが等しく底辺の比が12になので面積の比も12になります。全体の面積は ②= になるので、これも書き込んでおきます(後で問題を解く時に役立ちます)。 頂点から1回切り 中の面積比12だけでなく 全体の面積3を書くこと これが「底辺比と面積」の 入試問題を考えていく前に、「底辺比と面積比」の基礎知識(きそちしき)を確認(かくにん)していきましょう。 まずは基本形から。 《キホン1》 左の大きな三角形で、面積 S、T の比は? S : T = a : b になりますよね。 高さが同じだから、底辺比=面積比 になります。 簡単(かん >球の体積・表面積 公式 高校入試関数の難関入試問題を解説~第2回~ グラフから面積の比を考える! 高校入試対策 高校入試小数部分から式の値を求める問題! 高校入試対策 613 北海道高校入試数学18年の大問4(関数)を解説! 高校入試対策 14 高校入試
面積(英語: Area )是用作表示一個曲面或平面 圖形所佔範圍的量,可看成是長度(一維度量)及體積(三維度量)的二維類比。 對三維立體圖形而言,圖形的邊界的面積稱為表面積。 計算各基本平面圖形面積及基本立體圖形的表面積公式早已為古希臘及古中國 人所熟知。・三角形の面積(3辺の値:ヘロンの公式) 2 a b c s とすると,S s s a s b s c ・三角形の面積(内接円の半径rを用いて) 1 2 S r a b c ・三角比を用いた対称式 基本対称式(sin cos ,sin cos )で表す ※特にsin cos の形を見たら2乗してみる! ・円に内接する四角形 ①四角形を対角線で2 上野竜生です。三角形の面積比は線分比と密接な関係があります。これについて紹介します。 基本は三角形の面積の公式 三角形の面積の基本の公式は「底辺×高さ÷2」 ということは「底辺」「高さ」が等しい三角形の面積は等しいですし
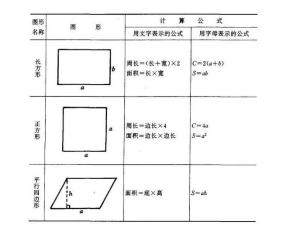
相似比とは、辺の長さの比でした。それでは面積や体積の比はどうなるのでしょうか。 相似比がabのとき 面積比=(a×a)(b×b) 体積比=(a×a×a)(b×b×b) 例えば長方形の面積は「たて×横」なので、たての長さも横の長さも2倍になれば「2倍×2倍」に 台形の面積の公式 台形の面積を 、高さを 、上底を 、下底を とすると、 (台形の面積) (上底 下底) (高さ)それでは「円の面積の公式」を使った「練習問題」を解いてみましょう。 練習問題① 半径が 2(cm)の円の面積を求めてください。ただし円周率を 314とします。 練習問題② 半径が 32(cm)の円の面積を求めてください。ただし円周率を 314とします。 練習問題③ 面積が (cm 2)の円の半径を




均一影片 例題 三角形底邊與面積的關係學習單 Shareclass




三角形高的计算公式 三角形的高计算公式 三人行教育网 Www 3rxing Org
面積の計算 ご意見・ご感想 ヘロンの公式を思い出し手計算を行いこのサイトで確認してみました。 a=103 b=635 c=425 で3615程度になるはずが6315というおかしな計算結果になるのはなぜでしょうか ? keisanより ヘロンの公式に当てはめると、 s=1045 になるので、面積の比はその共通角をはさむ2辺の積、 三角形abcの面積:三角形adeの面積=5×9:2×4=45:8 で求められるというものです。 この解き方を習っている場合は、 ア×3:イ×2=2:1 なので ア×3:イ×2=4:2=12:6 または「内項の積=外項の積」を利用して ア×3×1=イ×2×2 から、 ア=4、イ=3公式集 数学Ⅰ・A <式の計算> (6)相似な図形の面積比,体積比 相似比がmnである図形の面積比は、 m n 2 2 相似比がmnである立体の表面積の比は、 m n 2 2 , 体積比は、 m n 3 3 <集合> ベン図の利用と記号と用語の使用法を確実にする 属する: Îx A 共通部分: A B 和集合: A B 補集




这类几何证明题让很多学生不知所措 若思路清晰则解题毫无难度 网易订阅




朱式幸福 國中數學 梯形對角線形成的三角形面積比
・比表面積 (cm 2 /g)=表面積 (cm 2)÷質量 (g) ・比表面積 (1/cm)=表面積 (cm 2)÷体積 (cm 3)面積比の求め方を理解しよう こちら の記事で説明したように、 三角形の面積比は「(底辺の比)×(高さの比)」 で求めます。長方形の面積 平面図形 公式 集 確認シート a=長さ b =長さ h=高さ ℓ=弧の長さ S =面積 V =体積 四角柱 四角錐 三角柱 三角錐 円柱 円錐 空間図形 公式集 確認シート a=長さ b =長さ h=高さ ℓ=弧の長さ S =面積 V =体積 Created Date 9/2/08 AM



燕尾模型公式 万图壁纸网



圆的面积公式 Page19 西师大版六年级数学上册电子课本 教材 教科书 好多电子课本网
まとめ (1) 右図9ののように2つの三角形の底辺の比が ab ,高さの比が mn のとき,面積の比は ambn になる.(右の図9では高さの比を mn と読む.) (2) 右図10のような図形において,3つ以上の三角形の面積を比較するときは,次のように「比の値」を「分数」にすると簡単にできる.つまり、 相似比 \(ab\) の図形の面積の比は \(a^2b^2\) です。 なので 面積の比は \(a×ab×b\) となるわけです。 もちろん、三角形だけでなく、円や四角形や五角形やその他なんでも 相似な図形ならば、面積比は相似比の \(2\) 乗の比が成り立ちます。 例題1 下 三角関数の基礎知識。sinθ cosθ tanθ の覚え方・弧度法・三角比の表まとめ たとえば、「2本の対角線の長さが \(8,6\)、対角線の交わる角度が \(60°\) の四角形」の面積は \(S=\dfrac{1}{2}×8×6×\sin{60°}=12\sqrt{3}\) となります。 ③ ブレートシュナイダーの公式で求める 4辺の長さ \(a,b,c,d\) と対角の和



面积公式 搜狗百科



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻
面積比とは?公式と求め方 面積比(めんせきひ)とは、2つ以上の面積の比率です。下図をみてください。図形aの面積が5㎡、bの面積が10㎡です。このとき面積比=5:10=1:2です。 このままだと単に面積の値を比較しているだけですが、相似な図形の面積比は下記の公式があります。 相似比 あとは面積比を考えればおしまいですね。辺の比が分かっているので、面積比も求めることができます。 三角形 ABC の面積を S とすると、 $\mathrm{ BD }\mathrm{ DC }=54$ なので、三角形 ABD の面積は $\dfrac{5}{9}S$ 、三角形 ACD の面積は $\dfrac{4}{9}S$ となります。 円の面積の求め方 円の面積を求めるときは 円の面積 = 半径 × 半径 × 円周率 という公式を使います。 たとえば、半径が 3 c m の円の面積は 半径 半径 円周率 半 径 × 半 径 × 円 周 率 = 3 × 3 × 314 = 26 c m 2 と求めることができます。



Amc10 数学中的面积公式推证
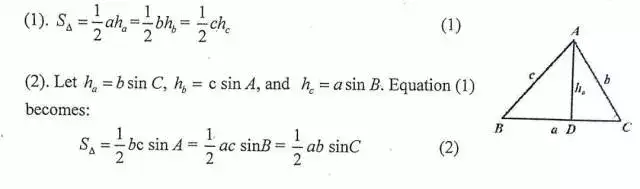



Amc 10 第一讲 数学中的面积公式都是怎么来的 知乎
四角形の面積 ・正方形の面積 1辺の長さから正方形の面積を計算します。 ・長方形の面積 縦と横の長さから長方形の面積を計算します。 ・台形の面積 上底と下底、高さから台形の面積を公式を使って計 面積比と線分比については、基礎編と、応用編があるにゃん 基礎編から読んで、次に応用編を読むのがオススメにゃん (基礎編)『 数学三角形の辺と面積の比について、2つの考え方をサクッとまとめました中学数学 図形 』



固定边长多边形的面积问题 Sqr5 S Blog




三角形abc向量求面积 通过三个点的坐标求出三角形面积的公式 三人行教育网 Www 3rxing Org



直角三角形面积公式 数学学习 宝贝宝贝网




內分點座標 分點公式 三分點公式 Easy Math Club



蝴蝶模型的面积比 蝴蝶模型面积公式 三人行教育网 Www 3rxing Org
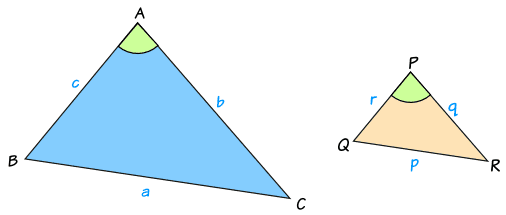



相似三角形定理




隨筆誌 重心面積公式證明




11等边三角形面积公式勾股定理初中数学初二 Youtube
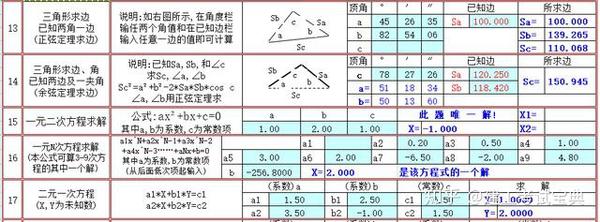



Excel函数公式大全 直接套用 计算速度计算器都比不上 快收藏 Excel函数圆面积公式 双偶网
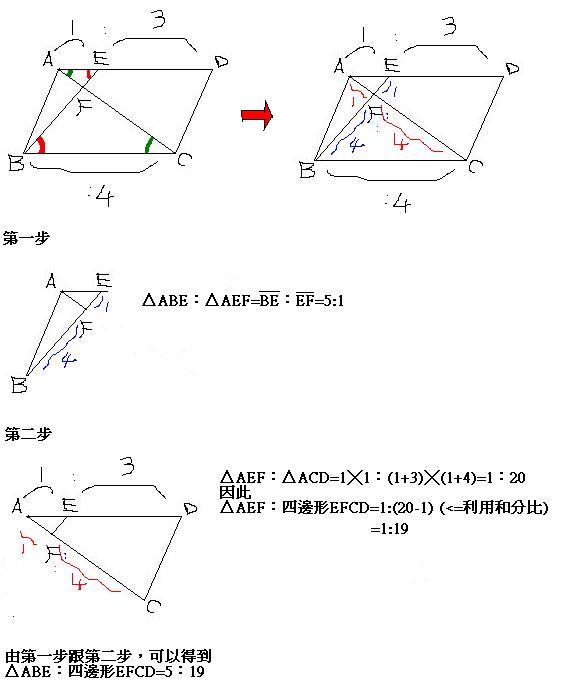



例題 三角函數 三角形面積公式 Iii 平面坐標與向量 高中的數學 Math Pro 數學補給站




三角形面積給我一個面積公式吧 Mikey Murph
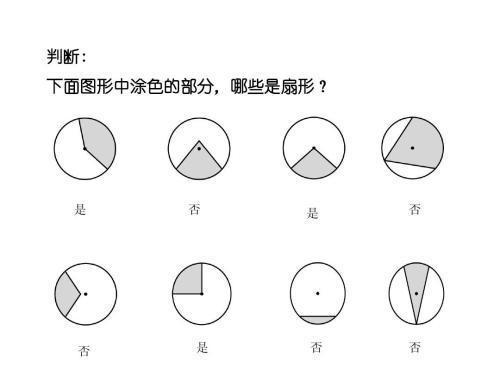



数学 扇形面积怎么推导来的 定积分求双纽线面积要用到 扇形面积角度积分公式 德涵网
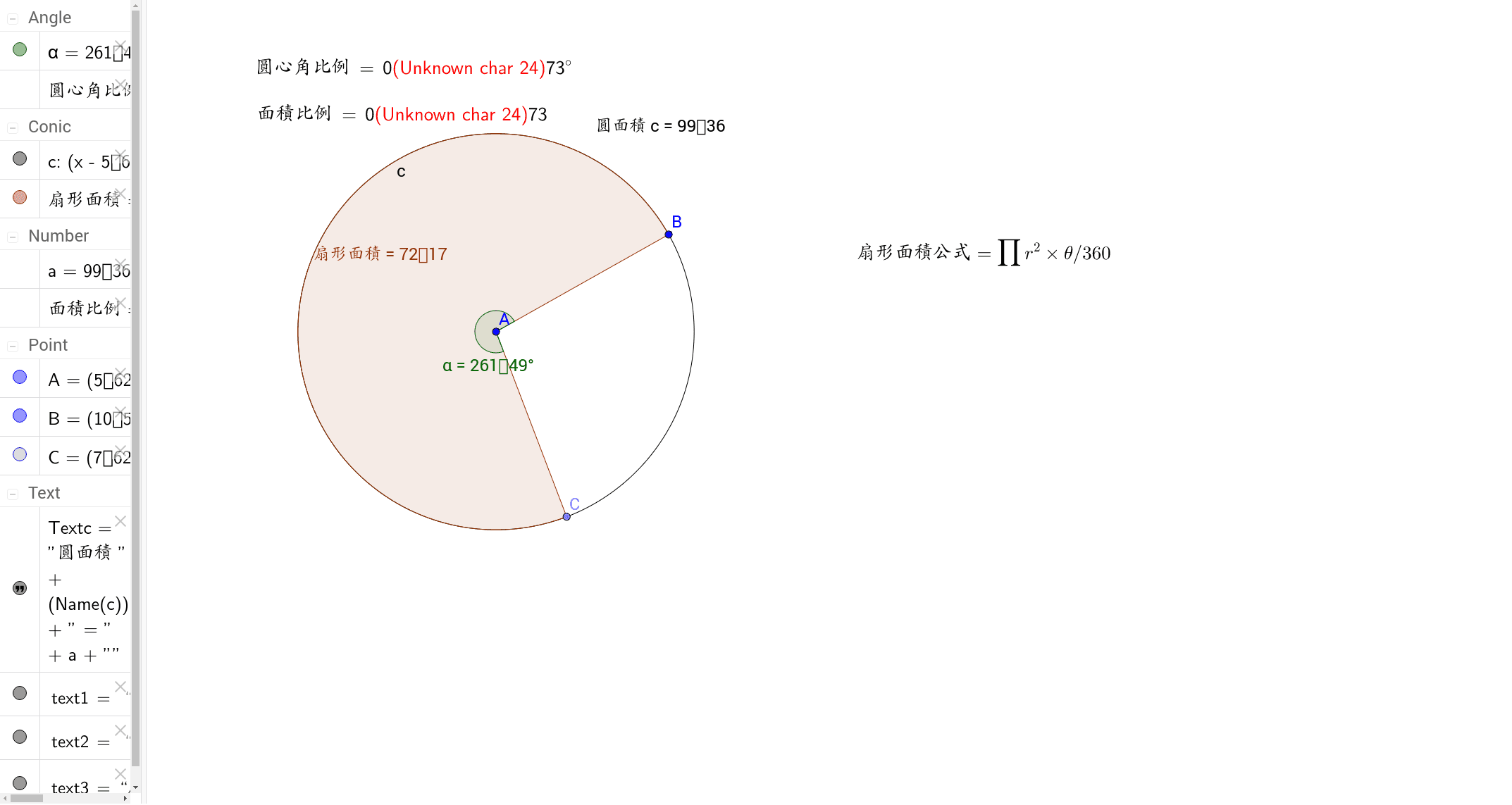



扇形面積公式 Geogebra



五年级数学上册6多边形的面积第五课时梯形的面积教案 新人教版 莲山课件




圓錐曲面面積公式圓錐的曲面面積的副本 Pbhcl




三角形已知边长求高公式 三角形求高为什么面积先要乘以2 图形面积计算公式教学的一些感悟 了不起频道的博客 Csdn博客




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




三十九讲五年级数学图形专题之两数同时加个数差值不变 手机网易网




三角形面積公式sin 三角形面積公式 Duph



圆的面积与半径平方之比是圆周率 这是数学证明结论 还是直觉 腾讯新闻




向量三角形面積向量公式前篇 Sahrz




直角三角形的邊長計算公式 國中的時候 數學課教我們如果一個三角形有一個直角 夾出這個直角的兩邊長度如果分別 By Anthony Liu Medium




相似三角形面积比



圆面积和周长公式 正多边形和圆 弧长公式及有关计算 尚书坊




三角形面積比公式png Image Transparent Png Free Download On Seekpng



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻
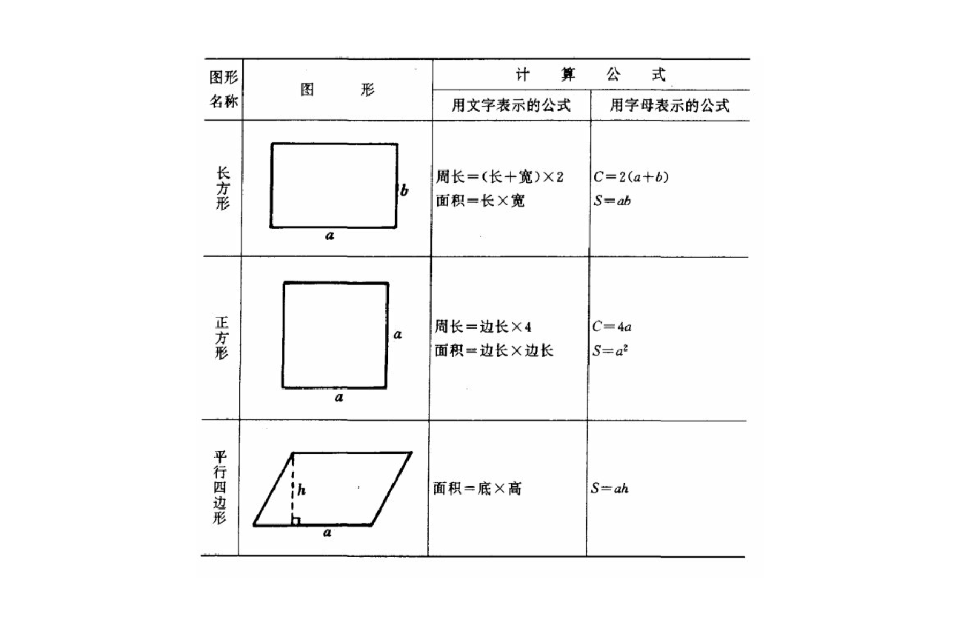



面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書




觀念 用平面向量求得面積公式 Youtube




Amc 10 第一讲 数学中的面积公式都是怎么来的 知乎



面积之比 燕尾定理模型 蝴蝶定理 梯形蝴蝶模型 共角模型 哔哩哔哩 つロ干杯 Bilibili




面积法44下载 Word模板 爱问共享资料
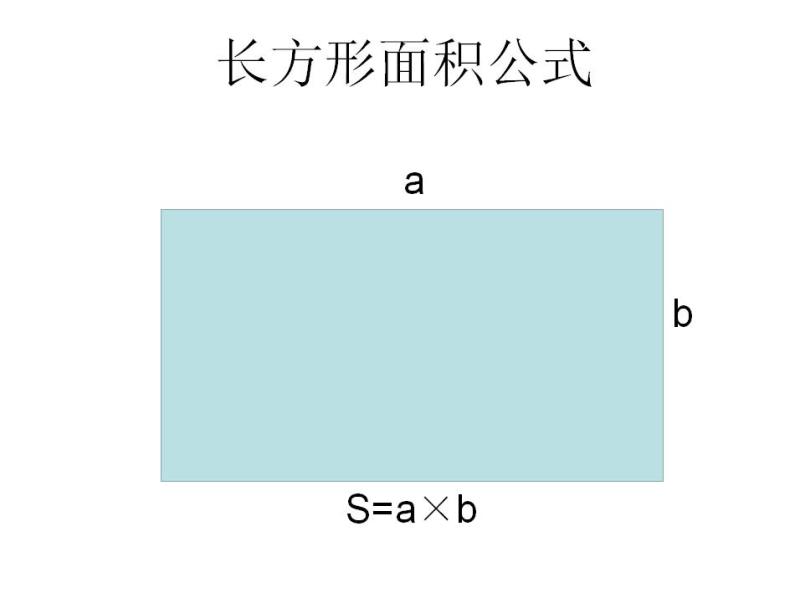



面积公式 搜狗百科



1
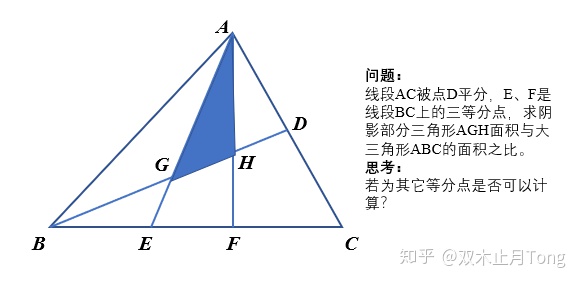



C 中计算三角形面积公式 看着有点迷的三角形面积计算 Weixin 的博客 Csdn博客



等边三角形面积公式 万图壁纸网




三角形の面積比 数学の偏差値を上げて合格を目指す




面积 搜狗百科




三角形面積秒殺法 有實力的你也值得擁有 就是快 每日頭條




面积问题 小奥的孩子也看过来吧 秒杀初中生 每日头条




相似三角形面積比與周長比 Youtube



Amc10 数学中的面积公式推证



三角形面积公式计算 万图壁纸网




高校入試対策数学 面積比に関する対策問題 Pikuu




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




梯形的面积公式




如何快速检查钢网开口面积比是否符合ipc7525



三角形周长公式 万图壁纸网




例題 相似三角形面積比的應用 數學 均一教育平台




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




Amc 10 第一讲 数学中的面积公式都是怎么来的 知乎



梯形面积公式换算 梯形形面积计算公式梯形形的面积公式三角形梯形面积公式 尚书坊




那些你不知道的技巧 四邊形分割後面積計算 Dsemathinfo




一道面積比公式的另證 的回響 用三角形的a S A 面積公式



这道小学数学图形题让很多同学束手无策 解题关键是运用整体法 文化资讯 娱乐新闻网



面积比问题1 哔哩哔哩 つロ干杯 Bilibili




面积公式 搜狗百科




这道初中数学几何题很简单 若不能理解该要点 则还是无法动笔 网易订阅



什么 任意四边形也有面积公式 海伦公式的推广及讨论 哔哩哔哩 Bilibili




皮克定理 维基百科 自由的百科全书




4种方法来计算三角形面积




4种方法来求六边形面积




三角形的几个面积公式都是什么时候发现的 网易订阅




坐标里求三角形面积的简单公式 拓展知识点 中学生可以学学 每日头条




基礎 相似三角形的周長比與面積比 數學 均一教育平台




Amc 10 第一讲 数学中的面积公式都是怎么来的 知乎



六年级不规则图形面积 西瓜视频搜索



1




直角三角形面積公式初中數學 畢氏定理 rbmi



圆面积公式大全 三角形面积计算公式大全及练习题 尚书坊



一类求三角形面积比向量问题的通法 手机版



相似三角形定理




單元12 三角比的性質




数学趣谈 球面积公式的不同导出方法 参考网



六年级三角形边长公式 西瓜视频搜索




相似三角形的面積比 Isdp08am 隨意窩xuite日誌




高二高中數學的 高二數學 三角形面積公式3 6 充實版 筆記 Clear




比例问题 五 算错了 那是因为没掌握好运算法 教育频道 手机搜狐



1




高一下數學三角形的性質比三角形面積正弦定理餘弦定理海龍公式 Clear




觀念 相似三角形的周長比與面積比 Youtube




常用圖形求面積計算公式 人人焦點
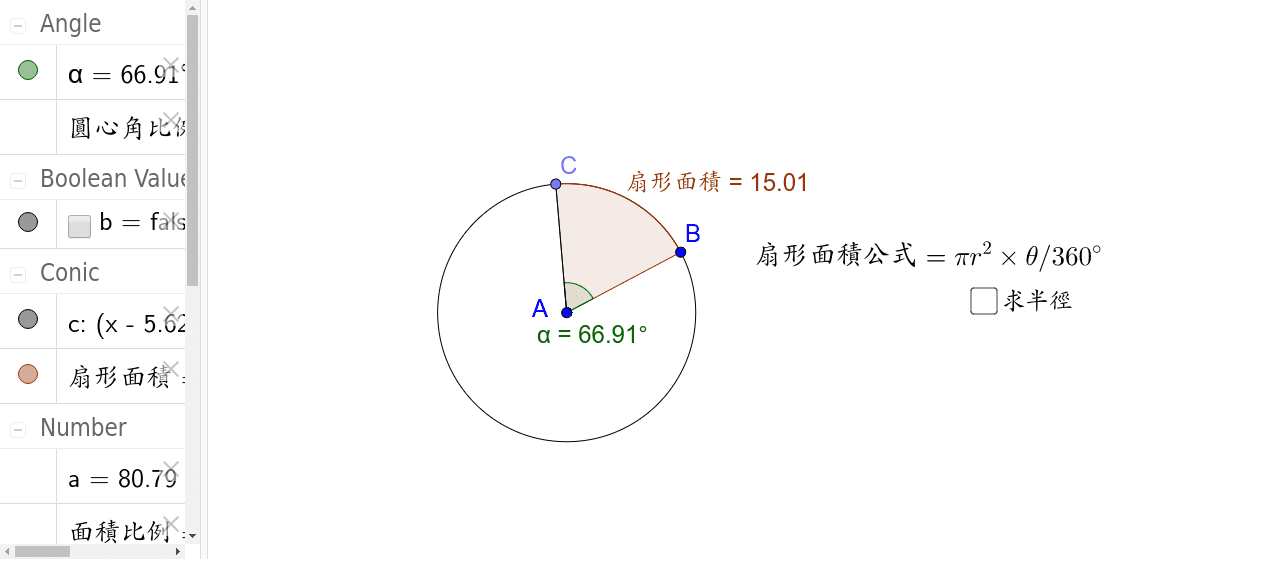



扇形面積公式2 Geogebra



1




如何快速检查钢网开口面积比是否符合ipc7525
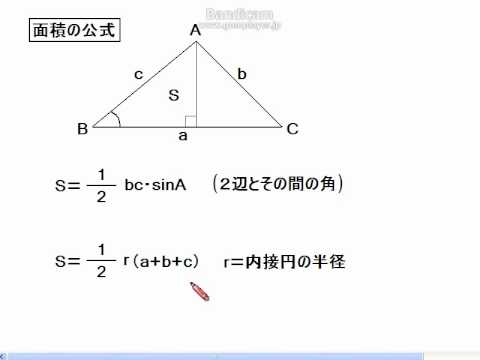



いちちの数学 三角比 面積の公式 Youtube




三角形的内切圆与外接圆面积之比 几何计算 华山青竹 博客园
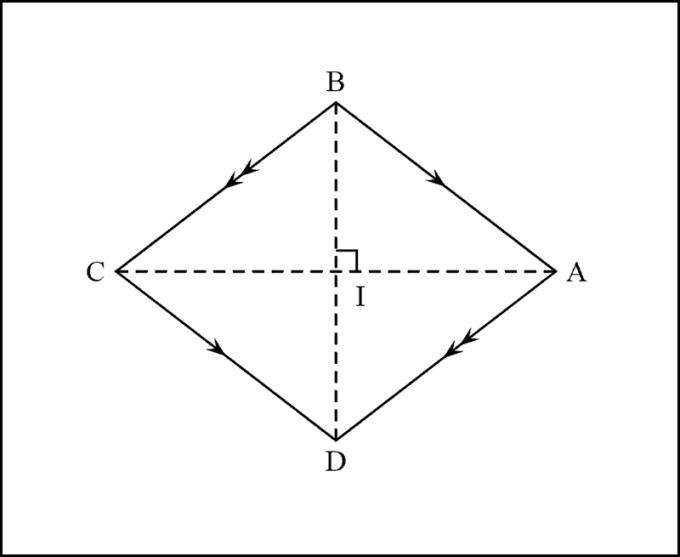



計算菱形確切面積 菱形周長的公式




三角形的内切圆与外接圆面积之比 几何计算 华山青竹 博客园



屏占比介绍 解释 什么意思 什么值得买
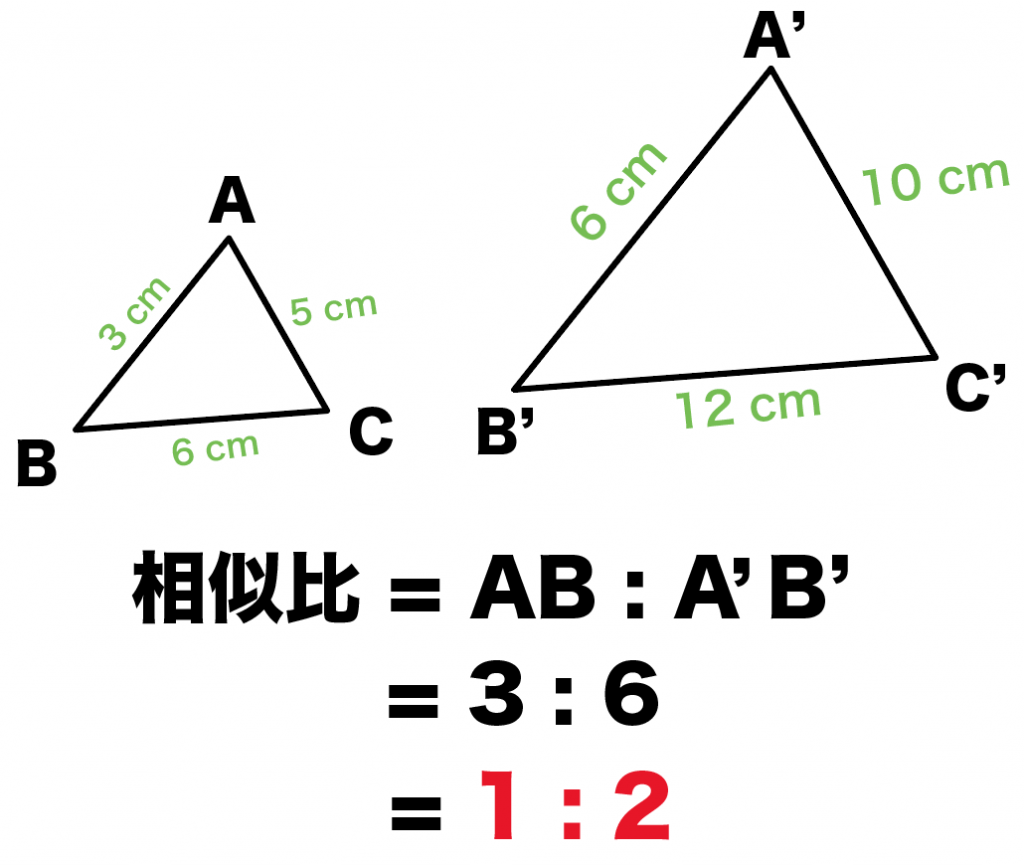



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




一道面積比公式的另證 的回響 用三角形的a S A 面積公式




相似三角形的面積比與邊長對應關係比 Live 多媒體數學觀念典online




等高三角形面積比 Youtube



平行四边形面积公式 平行四边形的面积计算公式 篆体字转换器


